Stage 5: HTU ÷ U (Bus Stop Method)
When children have conceptual understanding and fluency using the bus stop method without remainders, they can then progress onto ‘carrying’ their remainder across to the next digit.
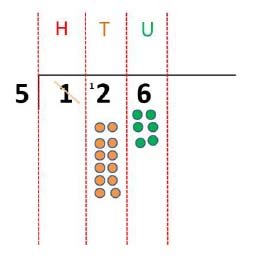
Place value counters can be used to support children apply their knowledge of grouping. (Dienes could also be used but place value counters are more efficient.)
Each digit as a multiple of the divisor
‘How many groups of 3 are there in the hundreds column?’
‘How many groups of 3 are there in the tens column?’
‘How many groups of 3 are there in the units/ones column?’

Formal Written Methods
Formal short division should only be introduced once children have a good understanding of division, its links with multiplication and the idea of ‘chunking up’ to find a target number (see use of number lines).
Short division to be modelled for understanding using place value counters as shown below. Calculations with 2 and 3-digit dividends.
Continued as shown, leading to the efficient use of a formal method. The language of grouping to be used
E.g. 1435 ÷ 6
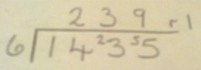
Children begin to practically develop their understanding of how to express the remainder as a decimal or a fraction.
Ensure practical understanding allows children to work through this (e.g. what could I do with this remaining 1? How could I share this between 6 as well?)
Please click on the link below to watch a video modelling the short division with no remainders strategy.
Short division with no remainders

